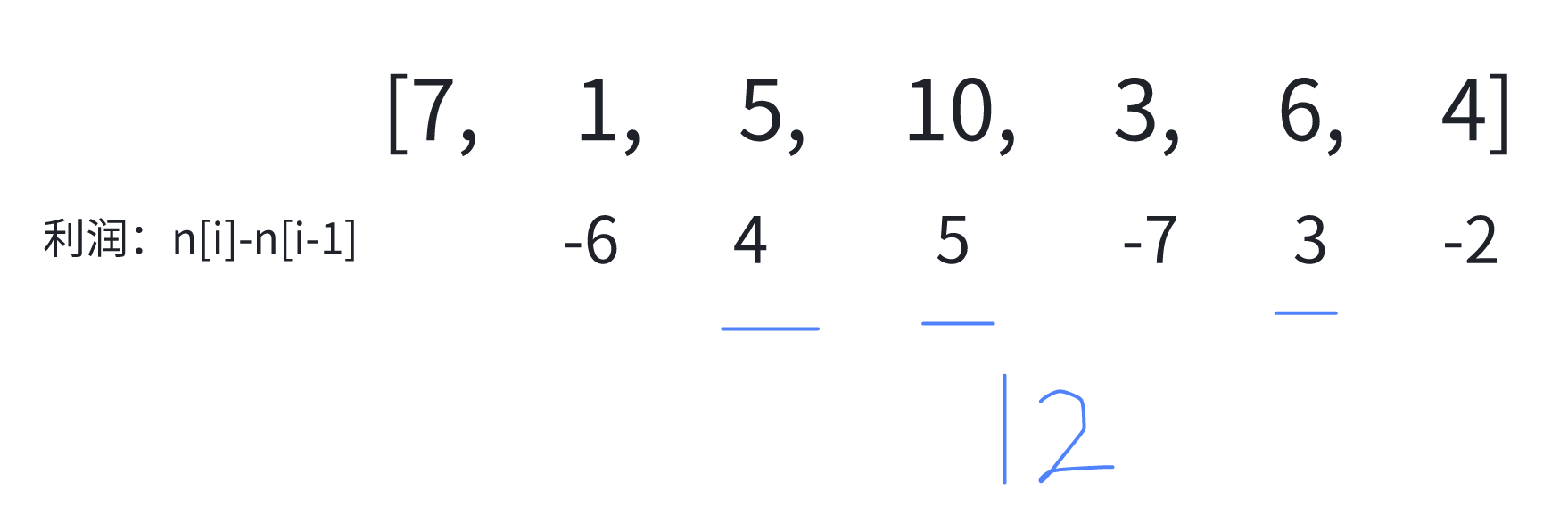Appearance
贪心
贪心算法理论基础
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
没了,这个只能靠感觉
1. 分发饼干
力扣题目链接https://leetcode.cn/problems/assign-cookies/description/假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j]。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是满足尽可能多的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。
所以你应该输出 1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出 2。
md
为了满足尽可能多的孩子,我们应该采用贪心策略:
1、将孩子的胃口值数组 `g` 和饼干尺寸数组 `s` 都进行升序排序
2、优先满足胃口小的孩子,这样可以保证整体能满足的孩子数量最多
3、使用双指针分别指向孩子和饼干,当饼干能满足孩子时,两个指针都向后移动,否则只移动饼干指针js
/**
* @param {number[]} g
* @param {number[]} s
* @return {number}
*/
var findContentChildren = function (g, s) {
// 从小到大排序
g.sort((a, b) => a - b)
s.sort((a, b) => a - b)
// 孩子指针
let child = 0
// 饼干指针
let cookie = 0
// 满足孩子数量
let count = 0
while (child < g.length && cookie < s.length) {
// 如果当前饼干能满足当前孩子
if (g[child] <= s[cookie]) {
child++
count++
}
// 无论是否满足,都要看下一个饼干
cookie++
}
return count
}2. 跳跃游戏
力扣题目链接https://leetcode.cn/problems/jump-game/description/给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
md
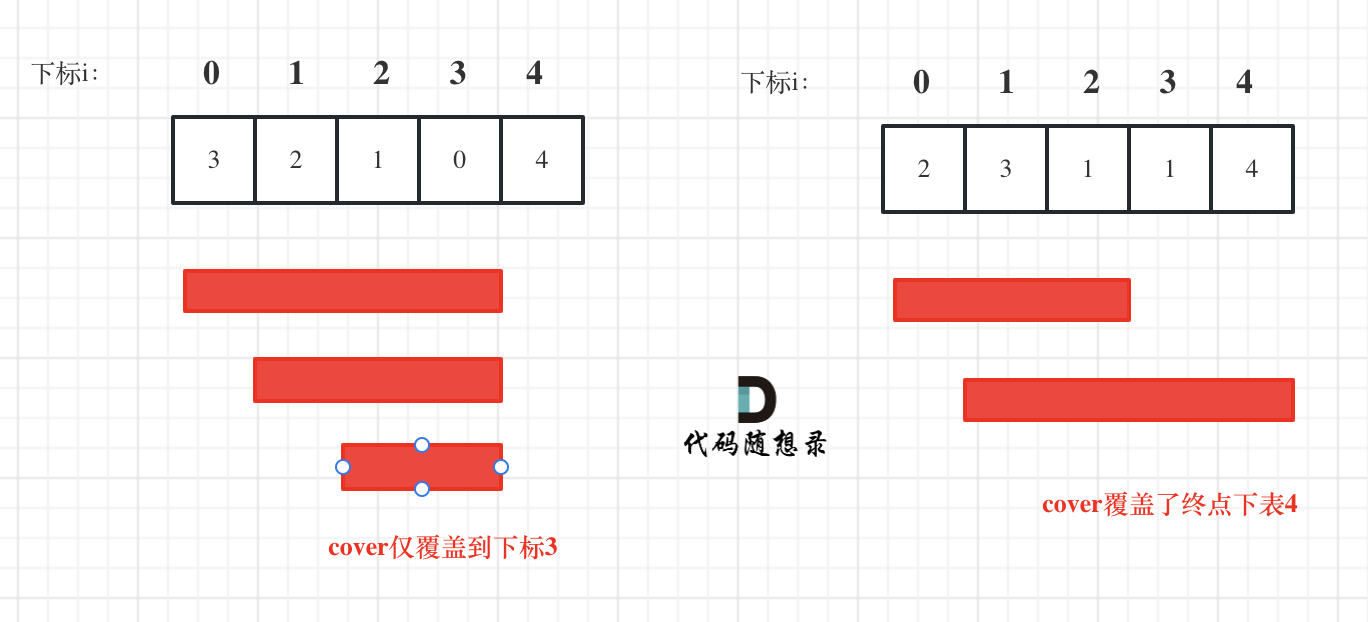
这道题其实跳几步无所谓,关键在于可跳的覆盖范围!
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。
这个范围内,别管是怎么跳的,反正一定可以跳过来。
**那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!**
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
过程如下图:
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
如果 cover 大于等于了终点下标,直接 return true 就可以了。js
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function (nums) {
let maxReach = 0 // 当前能到达的最远位置
for (let i = 0; i < nums.length; i++) {
// 如果当前位置不可达,直接返回 false
// 如果当前的最大距离还没有i大(正常情况是i<=maxReach,因为i每次只走一步),那后面就不可能到最后了
if (i > maxReach) {
return false
}
// 更新当前下标能到达的最远位置
maxReach = Math.max(maxReach, i + nums[i])
// 如果已经可以到达最后一个位置,提前返回
if (maxReach > nums.length) {
return true
}
}
return true
}
3. 跳跃游戏 II
力扣题目链接https://leetcode.cn/problems/jump-game-ii/description/给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在索引 i 处,你可以跳转到任意 (i + j) 处:
0 <= j <= nums[i]且i + j < n返回到达n - 1的最小跳跃次数。测试用例保证可以到达n - 1。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
c
本题的目标是用最少的跳跃次数到达数组的最后一个位置,使用贪心策略,每次尽可能地跳到最远的位置,这样可以保证跳跃次数最少。
具体实现时,维护三个变量:
- maxReach:当前能跳到的最远位置。
- end:当前这一跳能到达的最远位置。
- steps:跳跃次数。
- 遍历数组,更新 maxReach,当遍历到 end 时,说明需要进行下一次跳跃,此时更新 end 为 maxReach,并增加跳跃次数。
不需要具体知道每一步跳到哪,只需要知道每次跳跃能覆盖的范围边界,当走到边界时就必须再跳一次
if (i === end) {
end = maxReach // 更新下一次跳跃能到达的最远位置
steps++ // 增加跳跃次数
}
- 当 maxReach 大于等于最后一个位置时,返回当前的跳跃次数。js
/**
* @param {number[]} nums
* @return {number}
*/
var jump = function (nums) {
let maxReach = 0 // 当前能跳到的最远位置
let end = 0 // 当前这一跳能到达的最远位置
let steps = 0 // 跳跃次数
for (let i = 0; i < nums.length - 1; i++) {
// 更新当前能跳到的最远位置
maxReach = Math.max(maxReach, i + nums[i])
// 如果遍历到当前这一跳的最远位置,则需要进行下一次跳跃
/**
* 当我们遍历到 i === end 时,意味着我们已经走完了当前这次跳跃所能覆盖的所有位置,
* 此时我们必须进行下一次跳跃,所以需要增加跳跃次数
* (也就是当前走过的,也就是i步,和end持平,那么就该计算下一个跳跃了)
*/
if (i === end) {
end = maxReach // 更新下一次跳跃能到达的最远位置
steps++ // 增加跳跃次数
}
}
return steps
}4. 无重叠区间
力扣题目链接https://leetcode.cn/problems/non-overlapping-intervals/description/给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
注意 只在一点上接触的区间是不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
md
1、按区间结束位置排序:按照区间的结束位置进行升序排序,这样可以优先选择结束位置早的区间,为后续区间留出更多空间。
2、从第一个区间开始,选择结束位置最早的区间
3、遍历后续区间,如果当前区间的起始位置不小于上一个选中区间的结束位置,则选择该区间
总区间数减去选择的区间数,就是需要移除的最小区间数。js
/**
* @param {number[][]} intervals
* @return {number}
*/
var eraseOverlapIntervals = function (intervals) {
if (intervals.length === 0) return 0
// 按区间结束位置升序排序
intervals.sort((a, b) => a[1] - b[1])
let count = 1 // 选中的区间数量,初始化为1(选择第一个区间)
let end = intervals[0][1] // 上一个选中区间的结束位置
for (let i = 1; i < intervals.length; i++) {
// 如果当前区间起始位置大于上一个选中区间的结束位置,说明不重叠
if (intervals[i][0] >= end) {
count++
end = intervals[i][1] // 更新结束位置
}
}
// 需要移除的区间数 = 总区间数 - 选中区间数
return intervals.length - count
}5. 划分字母区间
力扣题目链接https://leetcode.cn/problems/partition-labels/description/给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。例如,字符串 "ababcc" 能够被分为 ["abab", "cc"],但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s(s 仅由小写英文字母组成)。
返回一个表示每个字符串片段的长度的列表。
示例 1:
输入:s = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的,因为划分的片段数较少。
示例 2:
输入:s = "eccbbbbdec"
输出:[10]
md
这道题需要先理清楚这个切割的过程,就拿:ababcbacadefegde 举例,
每个字母只能出现在一个字符串中,例如第一个字母 a,我们就需要找到他最后出现的位置,也就是下标 8 的位置,
如果在下标 0-8 的区间内,其余的字母也在这个范围,那么就可以分割一个字符串,
如果其余字符超过了这个区间,那么就扩大。
那么,如何去找到他们的最大区间呢?
我们可以利用哈希表,去记录字母出现的最远位置
如何去找切割点呢?
当我们 for 循环遍历的 i,等于我们的 end 结束位置时,说明这个区间已经结束,那么我们就可以进行切割了。js
/**
* @param {string} s
* @return {number[]}
*/
var partitionLabels = function (s) {
// 使用哈希表存储字符串中每个元素的最后出现的位置(也就是最远位置)
let endPosition = {}
for (let i = 0; i < s.length; i++) {
endPosition[s[i]] = i
}
// 记录每个切割的字符串长度
const res = []
// 切割字符串的开始下标
let start = 0
// 切割字符串的结束下标
let end = 0
for (let i = 0; i < s.length; i++) {
// 获取当前字符的最远下标
let max_position = endPosition[s[i]]
// 去更新当前切割字符串的结束下标
end = Math.max(end, max_position)
// 如果结束下标等于当前的i,标识当前切割的字符串已经结束
if (end === i) {
// 存放长度
res.push(end - start + 1)
// 更新起始值
start = end + 1
}
}
return res
}6. 买卖股票的最佳时机 II
力扣题目链接https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。 最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。 最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
TIP
这个题目在【动态规划】部分会单独再说,这里只举例一下如何用贪心算法解决。
md
这道题我们只需要去算出每天的利润,只去加为正的利润即可。js
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (prices) {
let total = 0
// i从1开始,0没有利润
for (let i = 1; i < prices.length; i++) {
const p = prices[i] - prices[i - 1]
if (p > 0) {
total += p
}
}
return total
}