Appearance
回溯
回溯法理论基础
什么是回溯法
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
回溯是递归的副产品,只要有递归就会有回溯。
回溯函数也就是递归函数,指的都是一个函数。
⚠️ 注意:回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,所以效率并不高。
但是有些问题没有更好的解决方案,只能用回溯法。
回溯法解决的问题
- 组合问题:N 个数里面按一定规则找出 k 个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个 N 个数的集合里有多少符合条件的子集
- 排列问题:N 个数按一定规则全排列,有几种排列方式
- 棋盘问题:N 皇后,解数独等等
⚠️ 注意:组合是不强调元素顺序的,排列是强调元素顺序。
例如:{1, 2} 和 {2, 1} 在组合上,就是一个集合,因为不强调顺序,而要是排列的话,{1, 2} 和 {2, 1} 就是两个集合了。
记住组合无序,排列有序,就可以了
如何理解回溯法
回溯法解决的问题都可以抽象为树形结构,因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N 叉树)。
回溯法模板
回溯函数模板返回值以及参数:回溯法的参数不容易在一开始就确定下来,可以在后面写逻辑的时候进行补充
回溯函数终止条件:什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
js
if (终止条件) {
存放结果
return
}- 回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。如图:
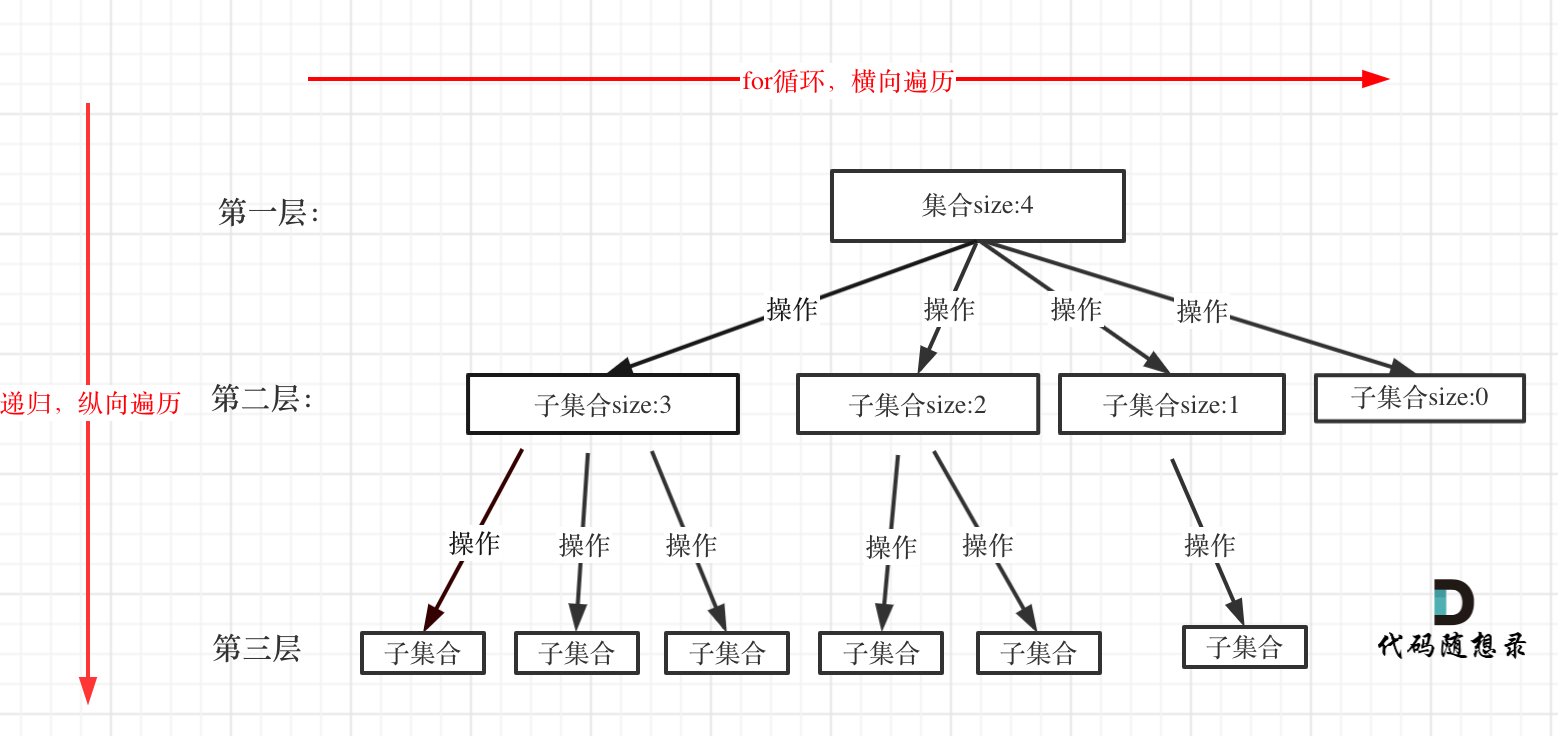
js
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}for 循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
模版:
js
function backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}1. 全排列
力扣题目链接https://leetcode.cn/problems/permutations/description/给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
注:nums 中的所有整数 互不相同
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]] 示例 3:
输入:nums = [1] 输出:[[1]]
md
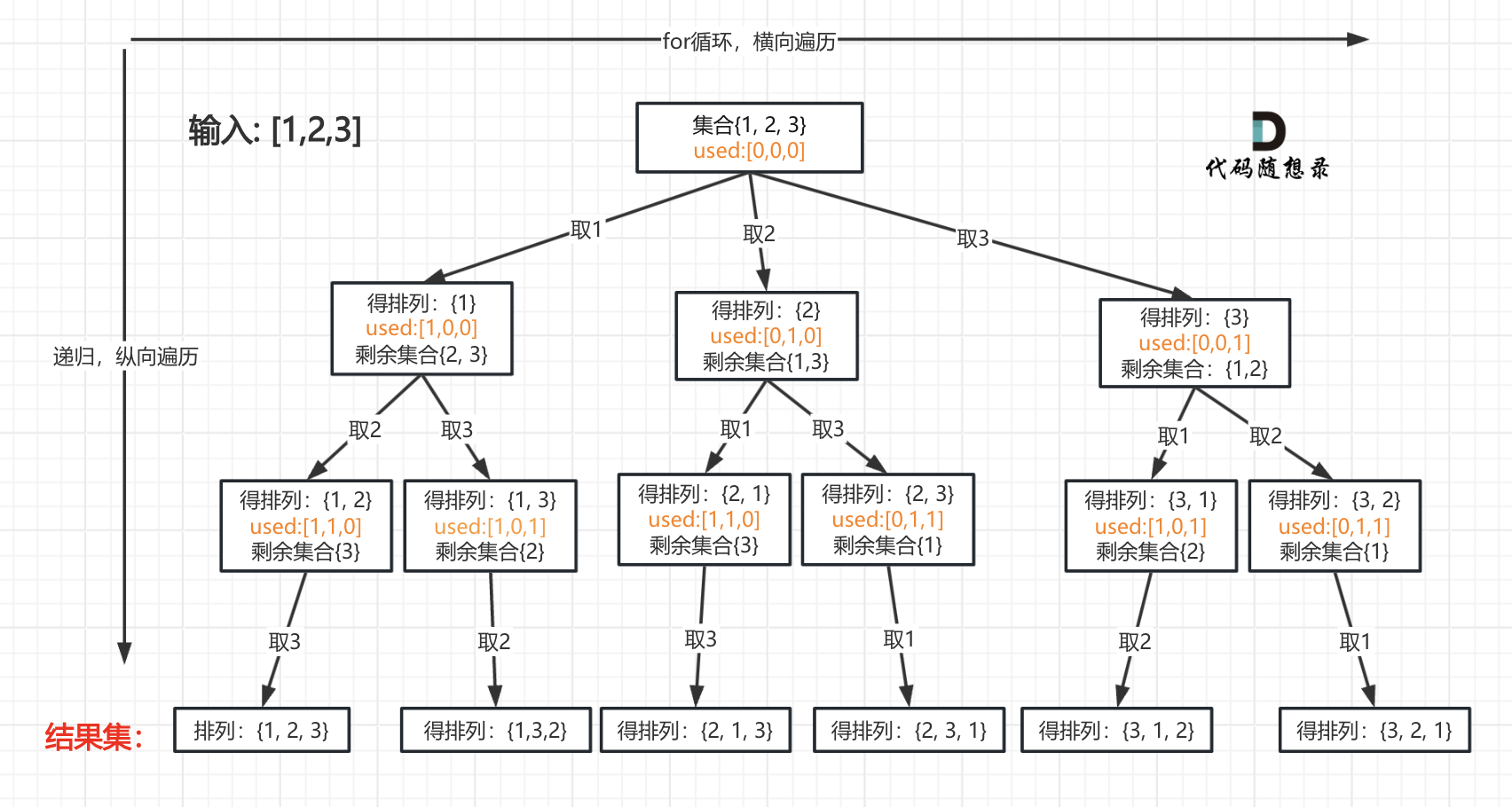
这道题看下面的图就可以知道思路,以[1,2,3]为例,如图:
竖方向上是递归,找到当前的排列可能,如第二层:1,2,3,
这时候需要记录一下哪些数字已经使用了,在横向 for 的时候,去递归这些未使用的数字,例如:
第二层的【1】,used 为[true, false, false],表示 1 已经使用,2、3 未使用,
去 for 循环 2、3,得到结果为:[1,2],[1,3],used 为[true, true, false],[true, false, true],
在[1,2]中 used 为 false 的只有 3 了,[1,3]中 used 为 false 的只有 2 了,继续递归;
当 path 的长度等于 nums 的长度时,返回 path,结束递归。
上面 for 循环过程中,如果元素不在 used 中,需要设置为 true,并且将该元素放入 path
(path 为某一种结果的过程内容)
> used 数组,其实就是记录此时 path 里都有哪些元素使用了,一个排列里一个元素只能使用一次。
还需要注意:递归后,需要回溯,也就是将 used 数组中该元素设置为 false,将 path 中该元素删除。
> 在递归搜索过程中,当一条路径探索完毕后,需要撤销之前做出的选择,以便能够探索其他可能的路径。js
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function (nums) {
// 存放结果的二维数组
const res = []
// 一维数组,记录当前路径(当前正在构建的排列)
const path = []
backtracking(nums, res, path, [])
return res
}
// used是记录元素是否在path中
function backtracking(nums, res, path, used) {
let len = nums.length
// 结束条件:当 path 的长度等于原数组长度时,说明找到了一个完整的排列,将其加入结果集 res。
if (path.length === len) {
// 切记:二维数组不能直接push
return res.push([...path])
}
for (let i = 0; i < len; i++) {
// 说明该元素已在当前路径中,跳过
if (used[i]) continue
// 加入路径,并将used[i]设置为true
path.push(nums[i])
used[i] = true
// 递归
backtracking(nums, res, path, used)
// 回溯(将内容还原)
used[i] = false
path.pop()
}
}
2. 子集
力扣题目链接https://leetcode.cn/problems/subsets/description/给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
md
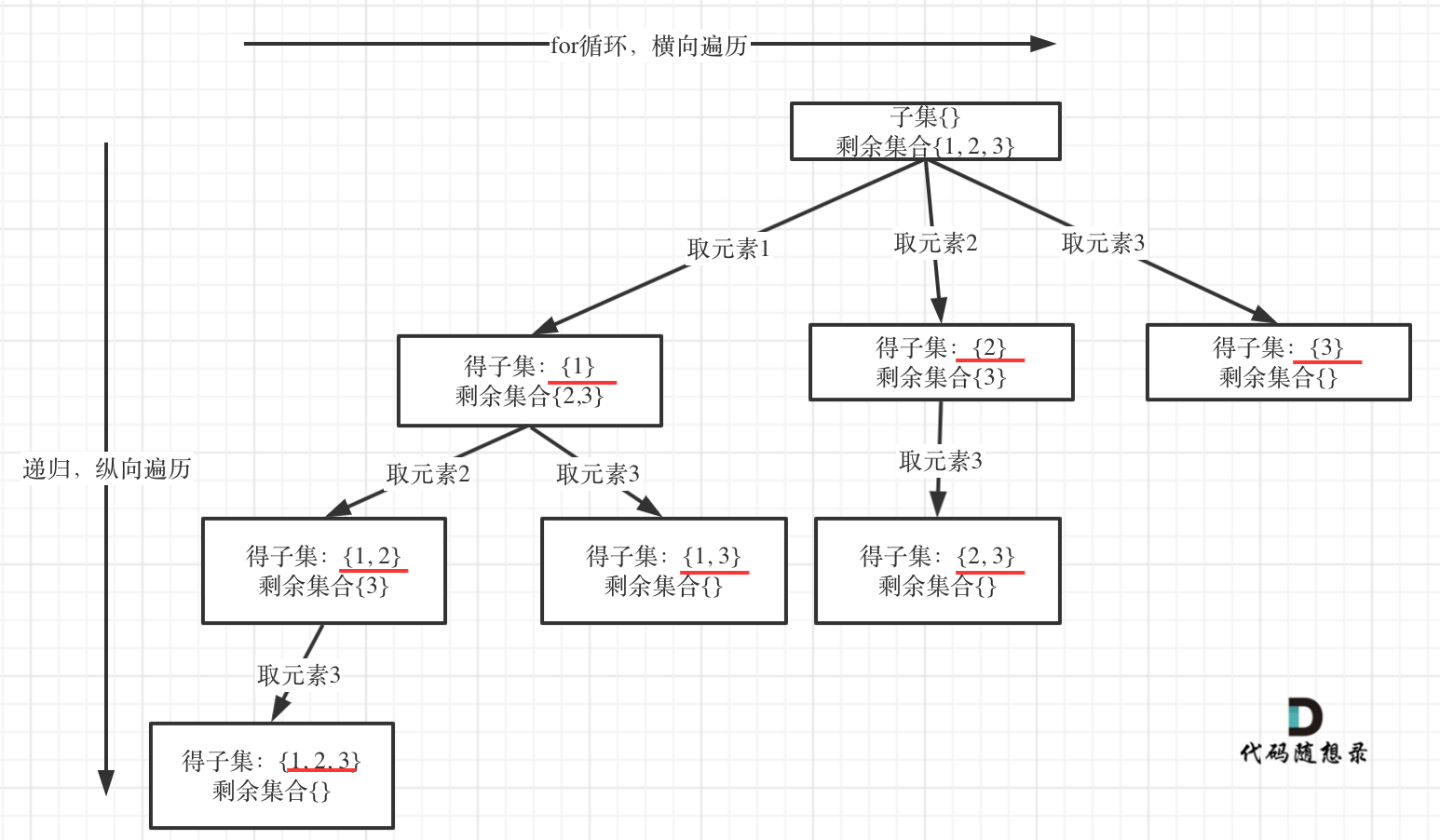
子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for 就要从 startIndex 开始,而不是从 0 开始!(和上一题不一样)
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
1、入参:nums、res(二维数组,存放最终结果)、path(一维数组,存放当前结果)、startIndex(遍历起点,因为取过的元素不用重复取)
2、递归终止条件:startIndex >= nums.length;startIndex 已经大于数组的长度了,就终止了,因为没有元素可取了;
其实也可以不加递归终止条件,因为 startIndex >= nums.length,本层 for 循环本来也结束了。
3、单层递归逻辑:
path.push(nums[i]); // 子集收集元素
backtracking(nums, res, path, i + 1); // 注意从 i+1 开始,元素不重复取
path.pop(); // 回溯js
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function (nums) {
// 存储结果的二维数组
const res = []
// 存储某一层树的结果,一维
const path = []
backtracking(nums, res, path, 0)
return res
}
function backtracking(nums, res, path, startIndex) {
// 每次递归都需要将当前路径加入结果(包括空集)
// 上一层的值,初始化没有为[]
res.push([...path])
// 当 startIndex 等于 nums.length 时,循环不会执行,自然结束递归
for (let i = startIndex; i < nums.length; i++) {
path.push(nums[i])
backtracking(nums, res, path, i + 1)
// 回溯
path.pop()
}
}
3. 电话号码的字母组合
力扣题目链接https://leetcode.cn/problems/letter-combinations-of-a-phone-number/description/给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
注:digits[i] 是范围 ['2', '9'] 的一个数字。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
c
这道题和第二题很相似,使用递归实现,需要解决的问题:
1、数字和字母如何映射:可以使用 map 进行映射
2、两个字母就两个 for 循环,三个字符我就三个 for 循环,以此类推:回溯法来解决 n 个 for 循环的问题,
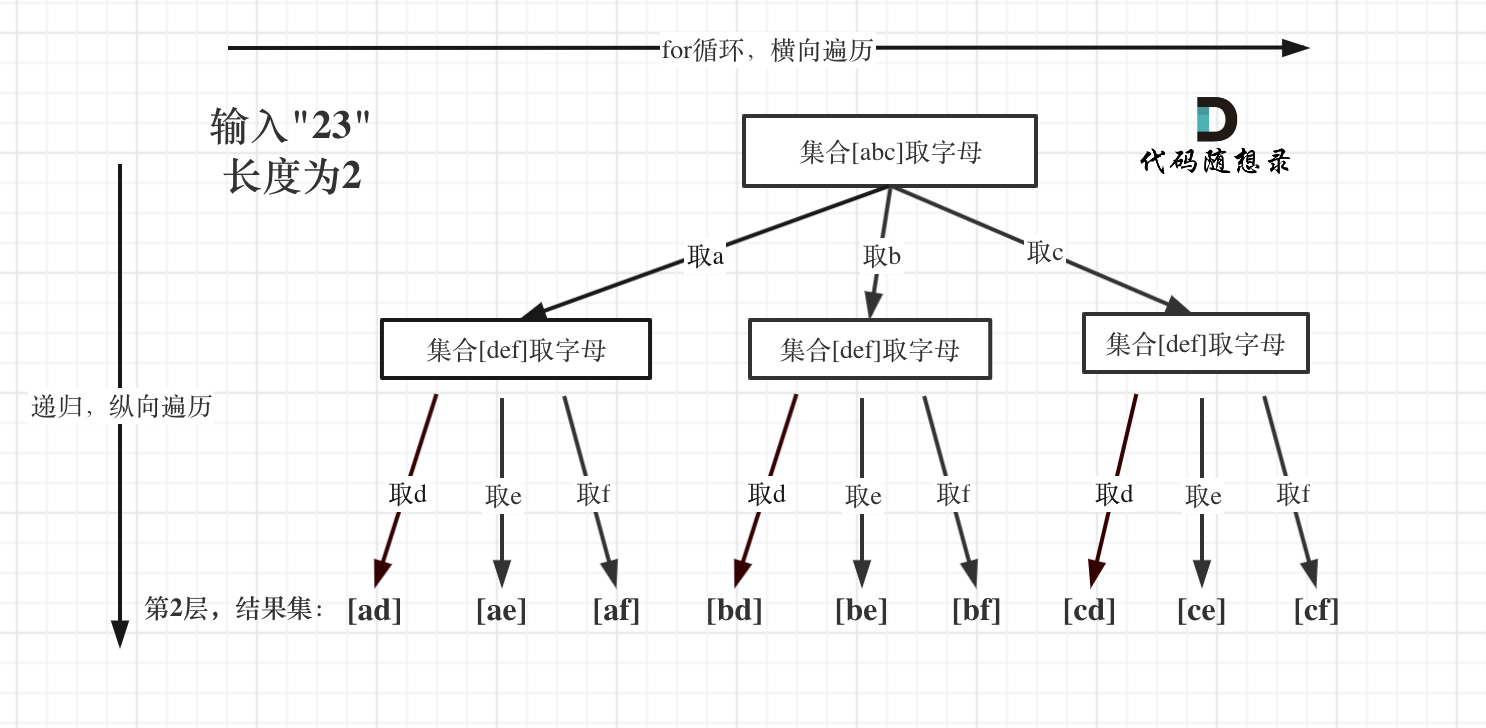
例如:输入:"23",抽象为树形结构,如下图所示:
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
3、输入 1 _ #按键等等异常情况:1, _, #等没有字母映射的按键,直接跳过处理下一个(虽然题目说是2-9的数字)
递归实现:
1、**确定参数**:需要一个字符串 s 来收集叶子节点的结果,然后用一个字符串数组 result 保存起来,还有一个是 index
⚠️ 注意:这个 index 可不是上一题的 startIndex 了。这个 index 是记录遍历第几个数字了,就是用来遍历 digits 的(题目中给出数字字符串),同时 index 也表示树的深度。
2、**确定终止条件**:例如:输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
那么终止条件就是如果 index 等于输入的数字个数(digits.length)了(本来 index 就是用来遍历 digits 的)。然后收集结果,结束本层递归。
if (index === digits.length) {
result.push(path.join(''));
return;
}
3、**确定单层遍历逻辑**:遍历当前数字对应的所有字母即可
const digit = digits[index];
const str = phoneMap[digit];
for (let i = 0; i < str.length; i++) {
path.push(str[i]);
backtrack(index + 1);
path.pop();
}js
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function (digits) {
// 处理空输入
if (!digits || digits.length === 0) {
return []
}
// 数字到字母的映射
const phoneMap = {
2: 'abc',
3: 'def',
4: 'ghi',
5: 'jkl',
6: 'mno',
7: 'pqrs',
8: 'tuv',
9: 'wxyz'
}
const result = []
const path = []
function backtrack(index) {
// 终止条件:已经处理完所有数字
if (index === digits.length) {
result.push(path.join(''))
return
}
const digit = digits[index]
// 获取字符串,例如2 => abc
const str = phoneMap[digit]
// 遍历当前数字对应的所有字母
for (let i = 0; i < str.length; i++) {
path.push(str[i])
backtrack(index + 1)
path.pop()
}
}
backtrack(0)
return result
}js
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function (digits) {
// 处理空输入
if (!digits || digits.length === 0) {
return []
}
// 数字到字母的映射
const phoneMap = {
2: 'abc',
3: 'def',
4: 'ghi',
5: 'jkl',
6: 'mno',
7: 'pqrs',
8: 'tuv',
9: 'wxyz'
// 1, *, # 等按键没有对应的字母
}
const result = []
const path = []
function backtrack(index) {
// 终止条件:已经处理完所有数字
if (index === digits.length) {
result.push(path.join(''))
return
}
const digit = digits[index]
const str = phoneMap[digit]
// 处理异常按键(1, *, #等没有字母映射的按键)
if (!str) {
// 跳过这些按键,直接处理下一个
backtrack(index + 1)
return
}
// 遍历当前数字对应的所有字母
for (let i = 0; i < str.length; i++) {
path.push(str[i])
backtrack(index + 1)
path.pop()
}
}
backtrack(0)
return result
}
4. 组合
力扣题目链接https://leetcode.cn/problems/combinations/description/给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
注意:
- 1 <= n <= 20
- 1 <= k <= n
示例 1:
输入:n = 4, k = 2
输出:
js;[ [2, 4], [3, 4], [2, 3], [1, 2], [1, 3], [1, 4] ]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
md
直接的解法当然是使用 for 循环,例如示例中 k 为 2,很容易想到 用两个 for 循环,这样就可以输出 和示例中一样的结果。
如果 n 为 100,k 为 50 呢,那就 50 层 for 循环,
此时就会发现虽然想暴力搜索,但是用 for 循环嵌套连暴力都写不出来!
回溯法解决的问题都可以抽象为树形结构(N 叉树),用树形结构来理解回溯就容易多了。
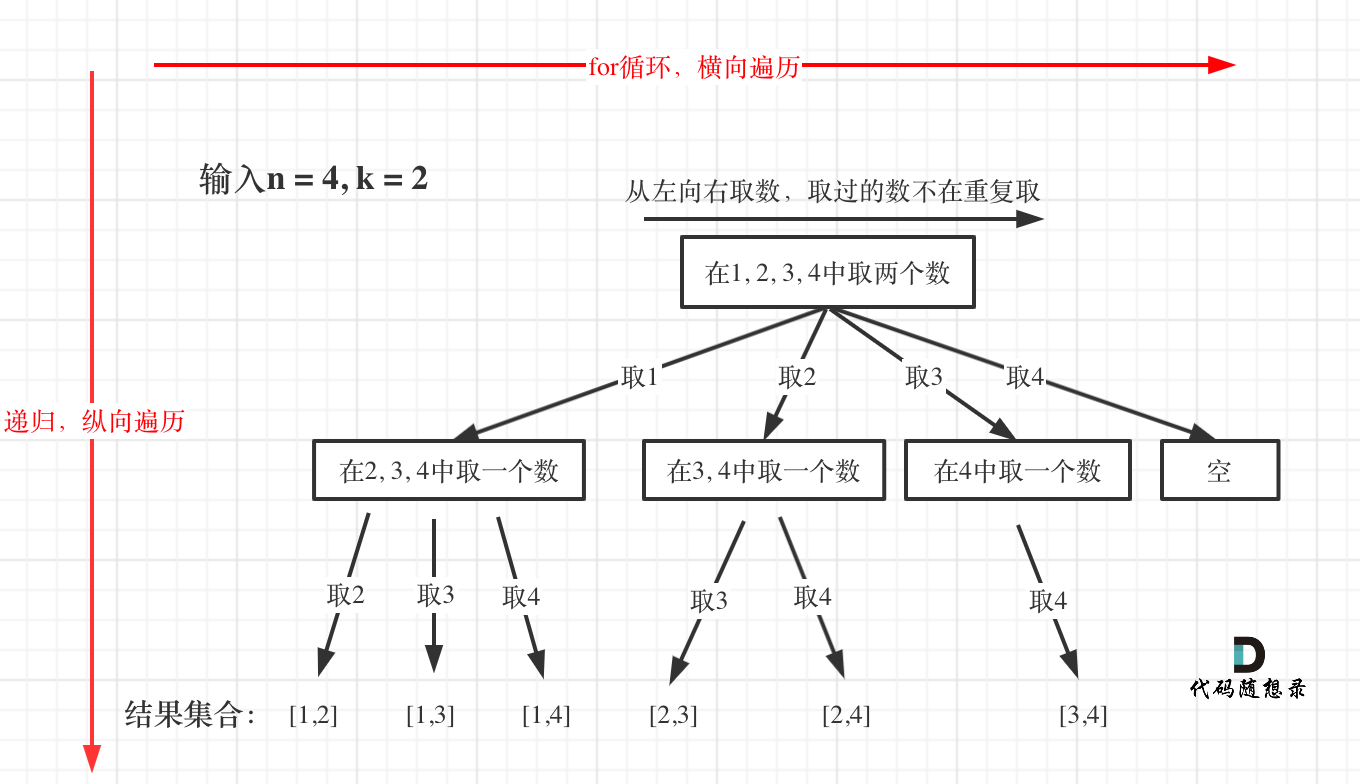
那么我把组合问题抽象为如下树形结构:
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
第一次取 1,集合变为 2,3,4 ,因为 k 为 2,我们只需要再取一个数就可以了,分别取 2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围。
图中可以发现 n 相当于树的宽度,k 相当于树的深度。
递归实现:
1、参数:res、path,最重要的就是 startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
startIndex 就是防止出现重复的组合
2、递归终止条件:path 这个数组的大小如果达到 k,说明我们找到了一个子集大小为 k 的组合了,在图中 path 存的就是根节点到叶子节点的路径。
3、单层逻辑:从图中可以看出 for 循环用来横向遍历,递归的过程是纵向遍历。
for 循环每次从 startIndex 开始遍历,然后用 path 保存取到的节点 ijs
/**
* @param {number} n
* @param {number} k
* @return {number[][]}
*/
var combine = function (n, k) {
// 存储最终结果(二维数组)
let res = []
// 存储每条结果(一维)
let path = []
function backtracking(startIndex) {
if (path.length === k) {
res.push([...path])
return
}
for (let i = startIndex; i <= n; i++) {
path.push(i)
// 例如:当前为1,下一层为【2,3,4】,所以就要递归搜索i + 1
backtracking(i + 1)
path.pop()
}
}
// 从1到n,初始化为1
backtracking(1)
return res
}
5. 组合总和
力扣题目链接https://leetcode.cn/problems/combination-sum/description/给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
注意:
- candidates 的所有元素 互不相同
- 1 <= target <= 40
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
c
递归思路:
1、参数:这道题和上一题一样,都是需要 startIndex 来控制 for 循环的起始位置
2、结束条件:sum等于target的时候,需要收集结果
if (sum > target) {
return;
}
if (sum == target) {
result.push(path);
return;
}
3、单层搜索的逻辑:单层for循环依然是从startIndex开始,搜索candidates集合
前面加了后面需要回溯减掉(path的push也是)
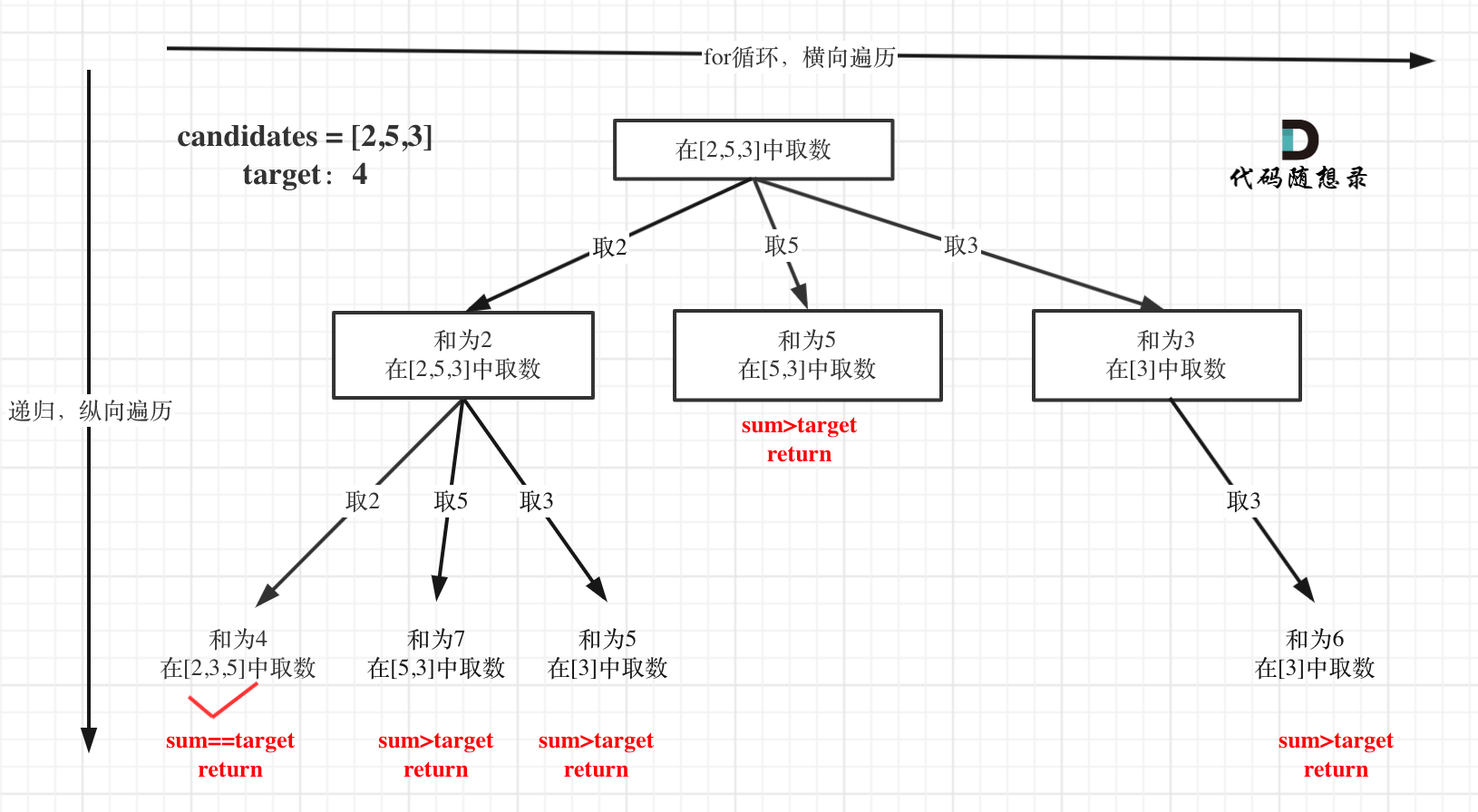
剪枝优化:对于sum已经大于target的情况,就没有必要进入下一层递归了,可以结束本轮for循环的遍历,这就是剪枝。
步骤如下图:js
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function (candidates, target) {
const res = []
const path = []
// sum提出来也行
// let sum = 0
function backtracking(startIndex, sum) {
// 剪枝:如果sum已经超过target,直接返回
// 必须要有这个剪枝操作,否则会栈溢出
if (sum > target) {
return
}
// 终止条件:找到目标和
if (sum === target) {
res.push([...path])
return
}
for (let i = startIndex; i < candidates.length; i++) {
// 处理当前节点
path.push(candidates[i]) // 添加到path
sum += candidates[i]
// 递归调用,注意这里是 i 而不是 i+1,因为可以重复使用元素
backtracking(i, sum) //传入 i 而不是 i+1
// 回溯
sum -= candidates[i]
path.pop() // 从path移除
}
}
backtracking(0, 0)
return res
}
何时需要 statrIndex?
- 如果是一个集合来求组合的话,就需要 startIndex,例如:【77.组合】
- 如果是多个集合取组合,各个集合之间相互不影响,那么就不用 startIndex,例如:【17.电话号码的字母组合】
在递归的时候,statrIndex 何时为 i,何时为 i+1?
递归调用参数的时候:backtracking(startIndex),分不清是 for 循环的 i,还是 i+1
- 组合问题,不允许重复使用元素:
backtracking(i+1) - 组合问题,允许重复使用元素:
backtracking(i)
6. 括号生成
力扣题目链接https://leetcode.cn/problems/generate-parentheses/description/数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
注意:1 <= n <= 8
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
md
生成有效括号的关键规则:
1、任意前缀中,左括号数量 >= 右括号数量(前缀是指:从字符串开始到任意位置的连续子串)
2、左右括号数量都等于 n
3、只有在左括号数量 > 右括号数量时,才能添加右括号js
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function (n) {
const res = []
function backtracking(left, right, path) {
// 终止条件(括号是成对出现的,所以要*2)
if (path.length === 2 * n) {
res.push(path)
return
}
// 添加左括号,只要不超过n,总是允许的
if (left < n) {
backtracking(left + 1, right, path + '(')
}
// 添加右括号,只有当右括号数量小于左括号数量时才允许
if (right < left) {
// 递归传入的right + 1,就是"左括号数量 >= 右括号数量"的体现
backtracking(left, right + 1, path + ')')
}
}
backtracking(0, 0, '')
return res
}js
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function (n) {
const res = []
const path = []
function backtracking(left, right) {
if (path.length === 2 * n) {
// 终止条件
res.push(path.join(''))
return
}
// 需要显式回溯
if (left < n) {
path.push('(')
backtracking(left + 1, right)
path.pop() // 显式回溯
}
if (right < left) {
path.push(')')
backtracking(left, right + 1)
path.pop() // 显式回溯
}
}
backtracking(0, 0)
return res
}显式回溯和隐式回溯
在上面【隐式回溯】这段代码中,我们确实没有像之前那样显式地执行回溯操作(如 path.pop()),这是因为字符串是不可变的值类型,而不是引用类型。
js
// 数组的情况(引用类型)
let path = []
path.push('(') // path 变成 ['(']
backtracking(path) // 传递的是引用
path.pop() // 必须手动回溯
// 字符串的情况(值类型)
let path = ''
let newPath = path + '(' // 创建新字符串 "(", path 本身没变
backtracking(newPath) // 传递的是新字符串
// 不需要手动回溯,因为原 path 没有改变在每次递归调用中:
path + '('创建了一个全新的字符串- 原来的 path 字符串并没有被修改
- 当递归返回时,自动回到之前的字符串状态
什么时候需要在回溯问题中使用 for 循环?
在之前的回溯问题中,我们使用 for 循环是因为:
需要在多个选项中做选择:
- 全排列:从 n 个数中选择一个未使用的数
- 子集:从数组中选择一个元素加入子集
- 组合:从 [1,n] 中选择一个数
- 电话号码:从当前数字对应的多个字母中选择一个
for 循环的作用:遍历当前层的所有可能选择
但在括号生成问题中比较特殊,每一步的选择是固定的:
只有两种选择:
- 添加一个左括号
( - 添加一个右括号
)
- 添加一个左括号
不需要遍历集合:我们不需要从一个集合中选择元素,只需要决定添加哪种括号
树形结构对比
组合问题:每层有多个分支,需要用 for 循环遍历。
txt
root
/ | | \
1 2 3 4
/|\ /|\ /|\
2 3 4 3 4 4括号生成问题的树:每层最多只有两个分支(添加左括号或右括号),可以直接用两个 if 语句处理。
txt
root
/ \
( (不合法)
/ \ / \
( ) ( )
/ \ / \ ... ...
( ) ( )7. 分割回文串
力扣题目链接https://leetcode.cn/problems/palindrome-partitioning/description/给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。
- 回文串是向前和向后读都相同的字符串。
- s 仅由小写英文字母组成
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
c
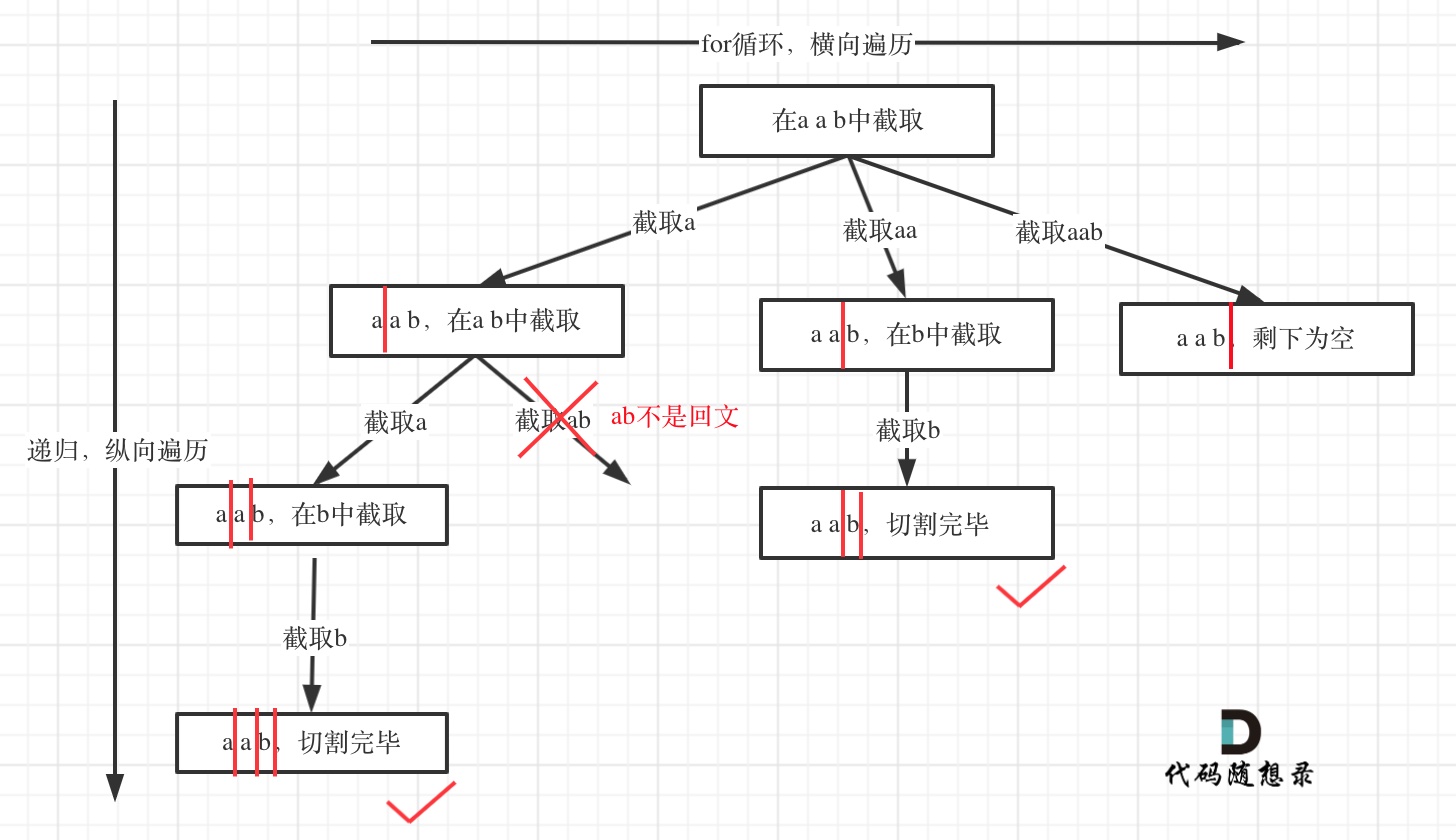
切割问题,也可以抽象为一棵树形结构,如下图:
递归实现:
1、确定参数:全局变量数组path存放切割后回文的子串,二维数组result存放结果集。(这两个参数可以放到函数参数里);
还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
2、确定终止条件:如下图,切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
3、单层递归逻辑:在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就用path来记录切割过的回文子串。
其次还需要判断是否是回文串,可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。js
/**
* @param {string} s
* @return {string[][]}
*/
var partition = function (s) {
// 存放最终结果的二维数组
const res = []
// 存放一条路径上的结果(一维数组)
const path = []
function backtracking(startIndex) {
if (startIndex >= s.length) {
res.push([...path])
return
}
for (let i = startIndex; i < s.length; i++) {
const str = s.slice(startIndex, i + 1)
// 如果不是回文串
if (!isPalindrome(str)) continue
path.push(str)
backtracking(i + 1)
path.pop()
}
}
backtracking(0)
return res
}
// 判断是否是回文串
function isPalindrome(str) {
let left = 0
let right = str.length - 1
while (left < right) {
if (str[left] !== str[right]) {
return false
}
left++
right--
}
return true
}
8. n 皇后
力扣题目链接https://leetcode.cn/problems/n-queens/description/按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
提示:1 <= n <= 9
示例 1:
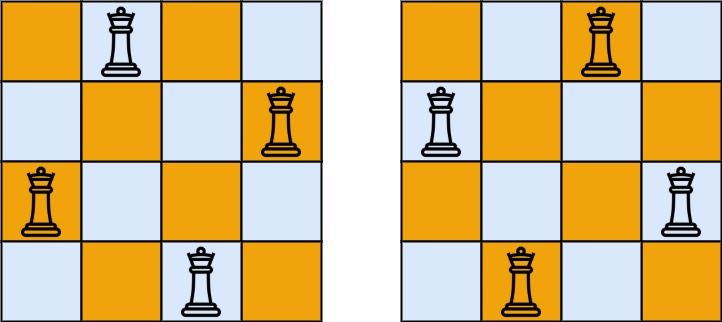
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
c
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
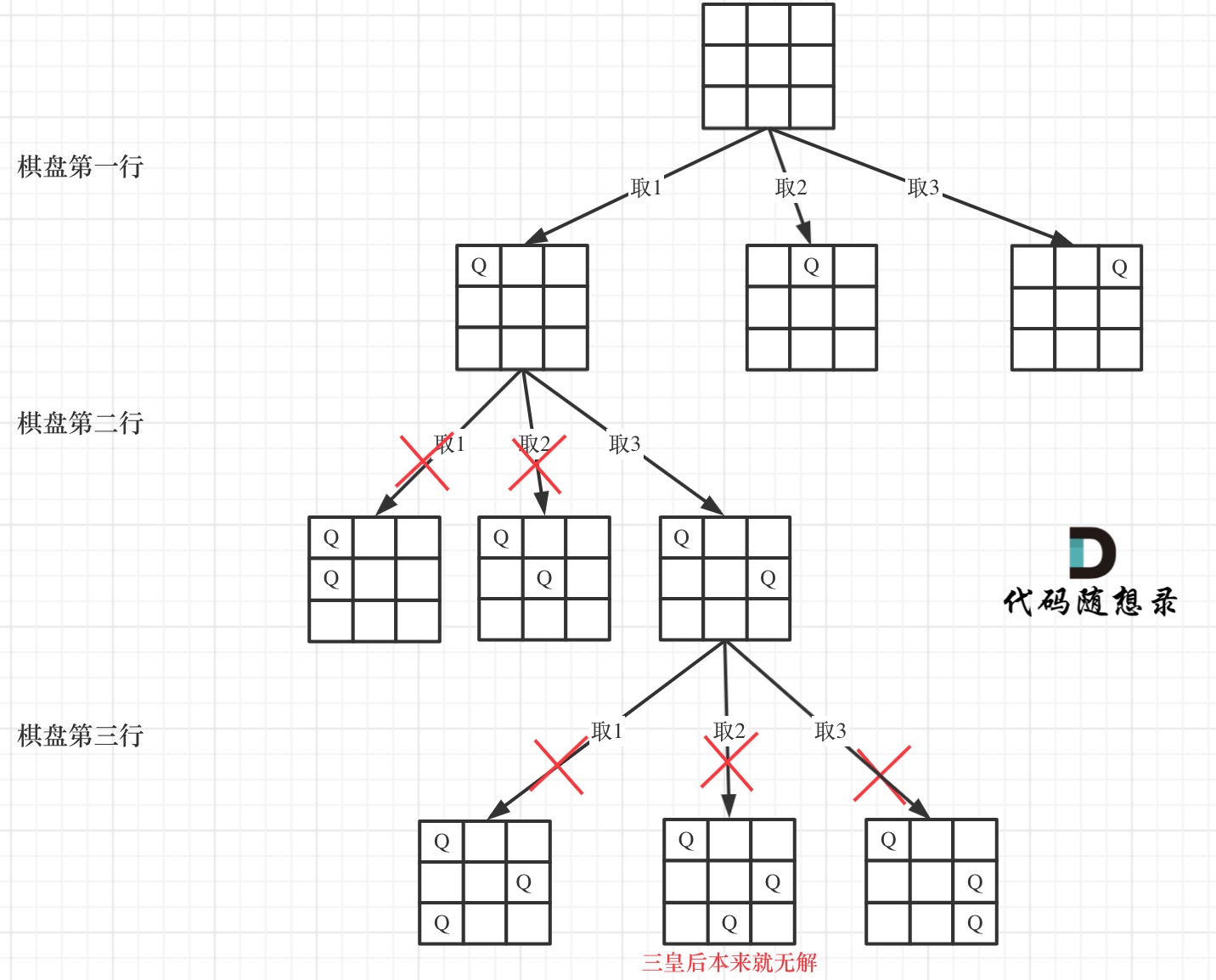
确定完约束条件,来看看怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如下图:
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
回溯实现:
1、确定参数:定义全局变量二维数组result来记录最终结果,参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了
2、递归终止条件:当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了
row相当于之前的startIndex,记录遍历到第几行了
if (row === n) {
result.push(chessboard);
return;
}
3、单层搜索的逻辑:遍历当前行的所有列
for (let col = 0; col < n; col++) {
if (isValid(row, col)) {
// 放置皇后
chessboard[row][col] = 'Q';
// 递归处理下一行
backtrack(row + 1);
// 回溯,移除皇后
chessboard[row][col] = '.';
}
}
还需要验证棋盘是否合法,按照如下标准去重(具体看代码):
1、不能同行
2、不能同列
3、不能同斜线 (45度和135度角)js
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function (n) {
// 存放最后结果(二维)
const res = []
// 矩阵(二维)
// ...
// ...
// ...
const chessboard = new Array(n).fill(0).map(() => new Array(n).fill('.'))
// 检查当前位置是否可以放置皇后
function isValid(row, col) {
// 检查列是否有皇后冲突
for (let i = 0; i < row; i++) {
if (chessboard[i][col] === 'Q') {
return false
}
}
// 检查左上对角线是否有皇后冲突
for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chessboard[i][j] === 'Q') {
return false
}
}
// 检查右上对角线是否有皇后冲突
for (let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] === 'Q') {
return false
}
}
return true
}
function backtracking(row) {
// 递归终止条件:当处理完所有行时,将当前解加入结果
if (row === n) {
// 将二维数组转换为字符串数组并加入结果
res.push(chessboard.map((rowArr) => rowArr.join('')))
return
}
// 遍历当前行的所有列
for (let col = 0; col < n; col++) {
if (isValid(row, col)) {
// 放置皇后
chessboard[row][col] = 'Q'
// 因为一行只能放一个,递归处理下一行
backtracking(row + 1)
// 回溯,移除皇后
chessboard[row][col] = '.'
}
}
}
backtracking(0)
return res
}